Applications
A generic application (app, for short) of beacon randomness is enabling public-verifiability of randomized procedures. For example, when randomly sampling for audits, auditors are prevented from biasing the selections (or being accused of it), and auditees are prevented from knowing the selections in advance (or being accused of it).
An interesting randomness/determinism duality: although beacon applications relate to the use of randomness, their public auditability requires a well specified deterministic operation (which then uses as input the needed random values).
The remainder of this page gives a few examples, at a high level, of applications of beacon randomness.
Generic procedure:
- Commit upfront: publish a statement \(S\) that explains the deterministic operation that will use the Beacon randomness (the output value randOut) from future time \(t\);
- Derive a seed: Get \(R={\tt randOut}[t]\) (from the pulse with timestamp \(t\)), and set the seed as \(Z=Hash(S||R)\)
- Perform the operation: Do what the statement \(S\) promised, using \(Z\) as the seed for all needed pseudo-randomness.
A possible refinement: To prevent even the Beacon from predicting the result of the seed \(Z\), the procedure statement \(S\) can be refined to also be a commitment of a secret value. Then, after the needed pulse is available, the application uses the secret value to derive the seed, and publicly reveals it or a ZK-proof that is has been properly used. That way not even a malicious beacon targeting the application could predict the result of the seed \(Z\).
Note: Real-life constraints can make this type of solution challenging, especially as it may require foreseeing procedures to adapt to unforeseen failure of selections (e.g., if a selected element is not available, a new one may have to be selected).
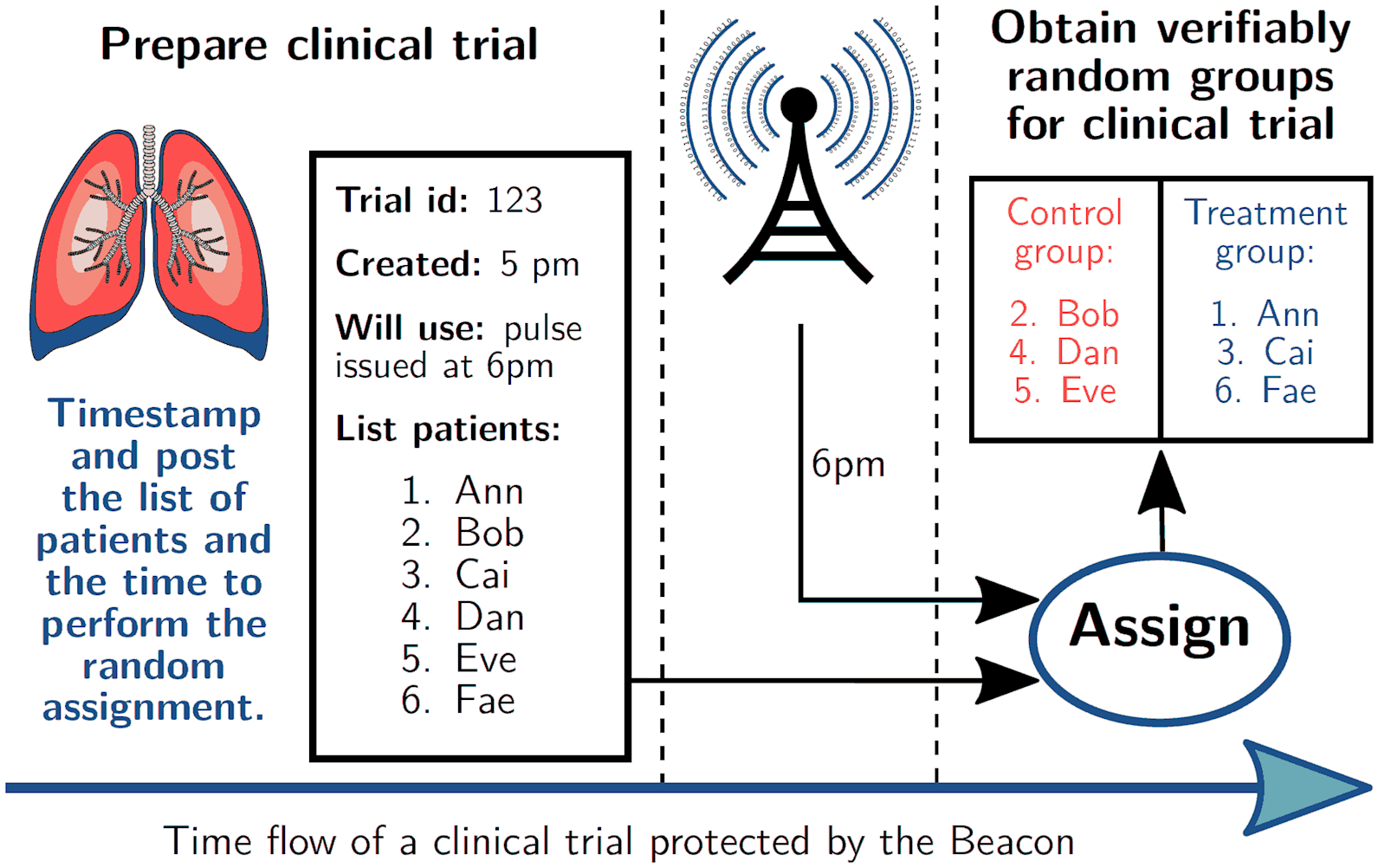
App example #1: Randomized clinical trials
Setting: a placebo-controlled clinical trial assigns patients to either the treatment group or the control group.
Goals: Enables select test and control groups for clinical trials; the public can check the trial was properly randomized.
Challenges: Apply commitments and zero-knowledge proofs to hide private data while proving correctness.
App example #2: Select random government officials for financial audits
(Example motivated by an application-project by the Random UChile Beacon)
Suppose a setting where a few subjects are to be selected from a large pool of candidates, with some weighting on private attributes. As a toy example, consider the following table of attributes, where a and b are abstract attributes (e.g., salary level and years on the job) that determine a risk score w. The probability of selection should be proportional to the risk score.
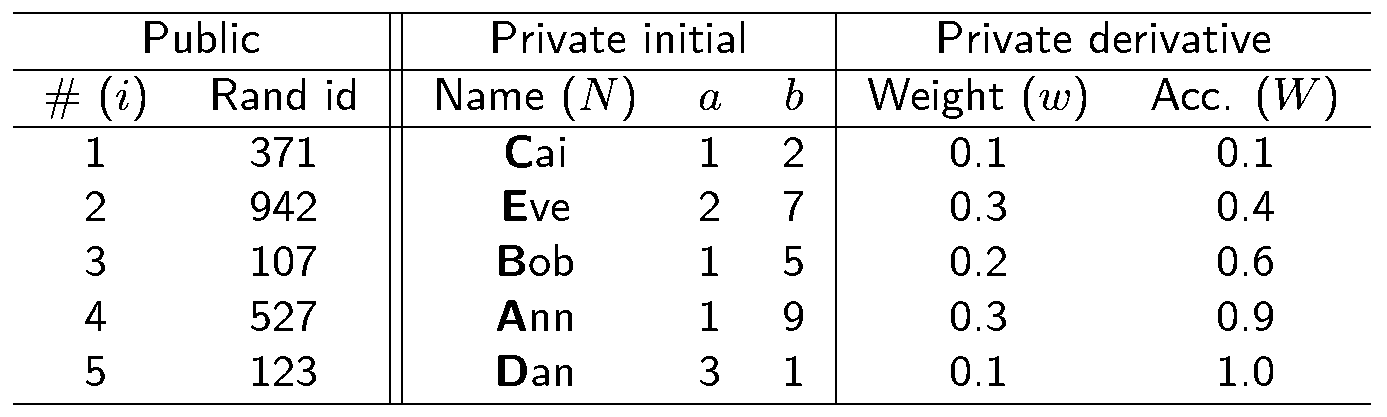
Procedure:
Commit to all attributes and publish the table of commitments ... then prove in ZK:
- \(a_i \in A\) (e.g., annual salary); \(b_i \in B\) (e.g., years in position);
- \(w_i = f(a_i,b_i)\)w_i = f(ai, bi) (correct probability weight);
- \(\sum_i w_i =1\) (correct sum of weights);
- \(W_i = w_i + W_{i-1}\) (correct accumulator);
- \(\{N_i\} = \textrm{NAMES}\) (non-repeated names from an appropriate set);
Following the procedure mentioned above, publish a statement \(S\) explaining the procedure that follows.
At the specified future time \(t\), derive a random \({\color{blue}R}:0<{\color{blue}R}\leq 1\) (random) from the Beacon and determine \(\#\red{j}: W_{max(1,\red{j}-1)} < {\color{blue}R} \leq W_{\red{j}}\)# j: Wmax(1,j−1) < R ≤ Wj
Prove in ZK that \(\red{j}\)j is consistent with \({\color{blue}R}\) and the table of commitments
Some references: slides 2020
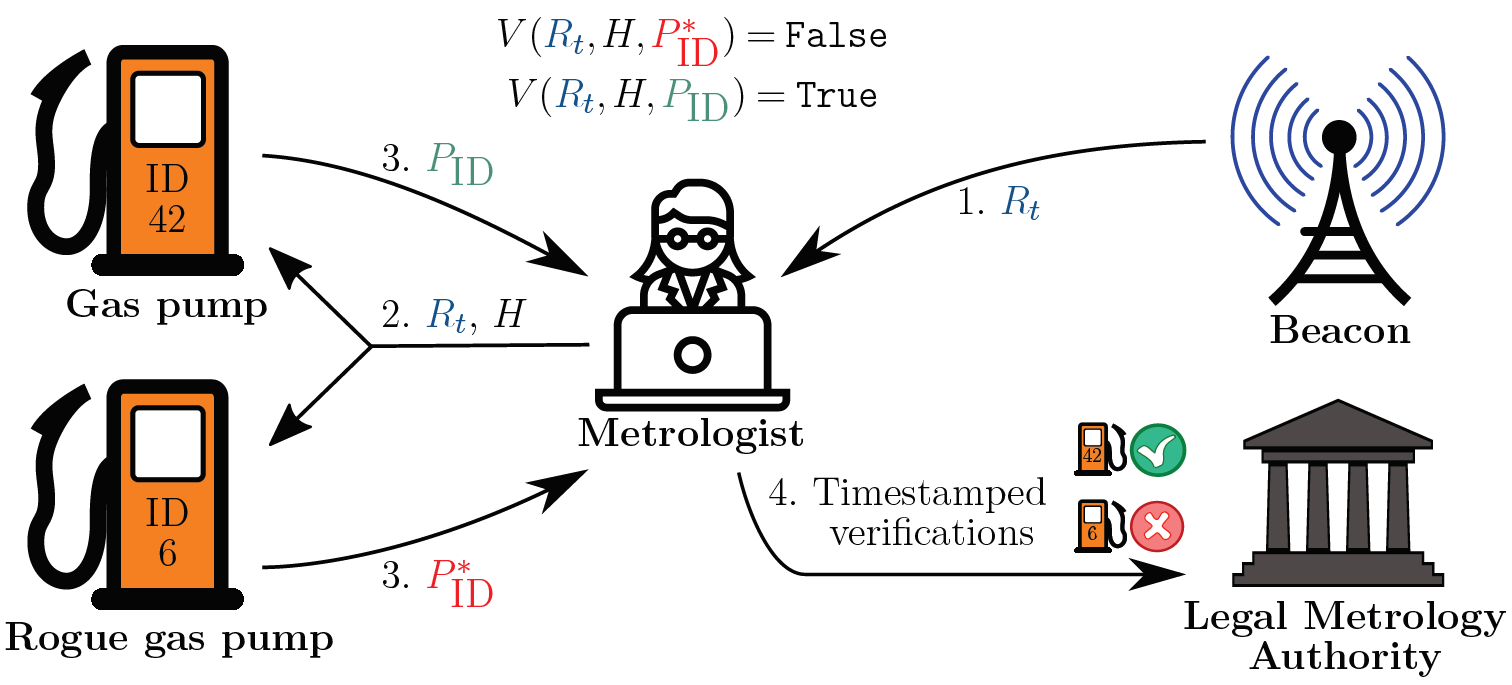
App example #3: Freshness of proofs in legal metrology
Goal: Ensure freshness of proofs of software possession by measuring instruments.
A system employs zero-knowledge proofs of knowledge to enhance security in a system of measuring instruments. Beacon randomness is used to ensure unpredictability of the challenges and freshness of the proofs.
Some references: poster 2020, ZKASP paper (earlier version appeared at OIML)
Examples of other possible apps:
- Judge selection. Defenders and prosecutors verify unbiased assignment of a judge to a court case, avoiding forum shopping.
- Quality control. Sample random lots for quality-measuring procedures, preventing auditors from biasing selections (or being accused of it), and preventing auditees from learning in advance which items “will be” selected. The use of a beacon facilitates the audit trail for later verification of the sample selection.
- Lotteries. Provide entropy to digital lotteries.
- Randomized security checks. When faced with "You have been randomly chosen for additional security screening", individuals would be able to confirm that the selection was really random.
Some references: poster 2019, poster 2021

